What does AM stand for? Maybe Ante Meridiem, before noon. Or maybe the element Americium (Am). Maybe it’s Artium Magister, a Master of Arts degree. Whatever the case, if you compound masters of the arts over time, you get Arctic Monkeys.
In 2013, Arctic Monkeys released their fifth studio album, AM. While the title references the band’s name, the cover art says otherwise. Taking inspiration from Velvet Underground’s cover art of volume units (VU), AM’s cover art is a wave with changing heights—amplitude modulation (AM).
As a recreational mathematician, I looked around the internet, trying to find a decent recreation of the AM cover as a graph, but none of them were good enough. Most stopped at just modulating a sine wave with a broader sine wave, but this method misses one crucial detail: the AM in the middle. Job Bouwman inserts the AM in the middle, but the heights and widths of the letters don’t quite match the cover.
The Arctic Monkeys weren’t just monkeying around with amplitude modulation. They figured out a clever way to seamlessly insert their initials into the graph. Mark my words, I will do the same. I will recreate the AM cover.
Rather than spending lots of time setting up a Jupyter Notebook and writing lots of Python code to establish a working development environment, I’m using Desmos. I believe the initial concept art began with a standard modulation of a sine wave inside a sine wave, so I am starting the same way.

Aha! See? In the center? There is a segment of the graph that can be used for the AM. I’ll mark it in green. This will require removing that purple part, which I see as a bonus. The A and M in the cover have longer wavelengths than the rest of the graph, so stretching the green segment should recreate this well.
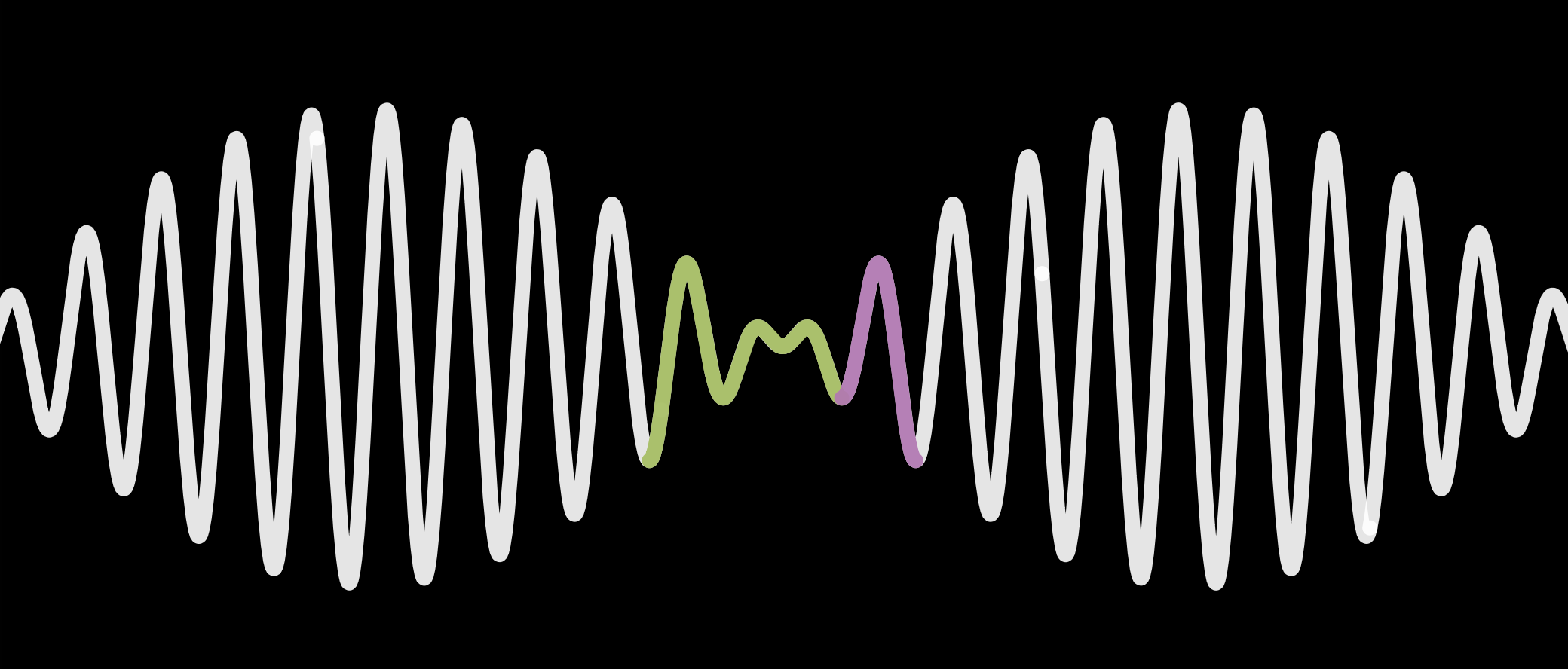
After stretching the green segment of the graph, the height of each portion will need to be adjusted. Maybe I’m just throwing a hammer at a screw, but a sigmoid function looks like it will do the trick. A few adjustments later, and we have this:
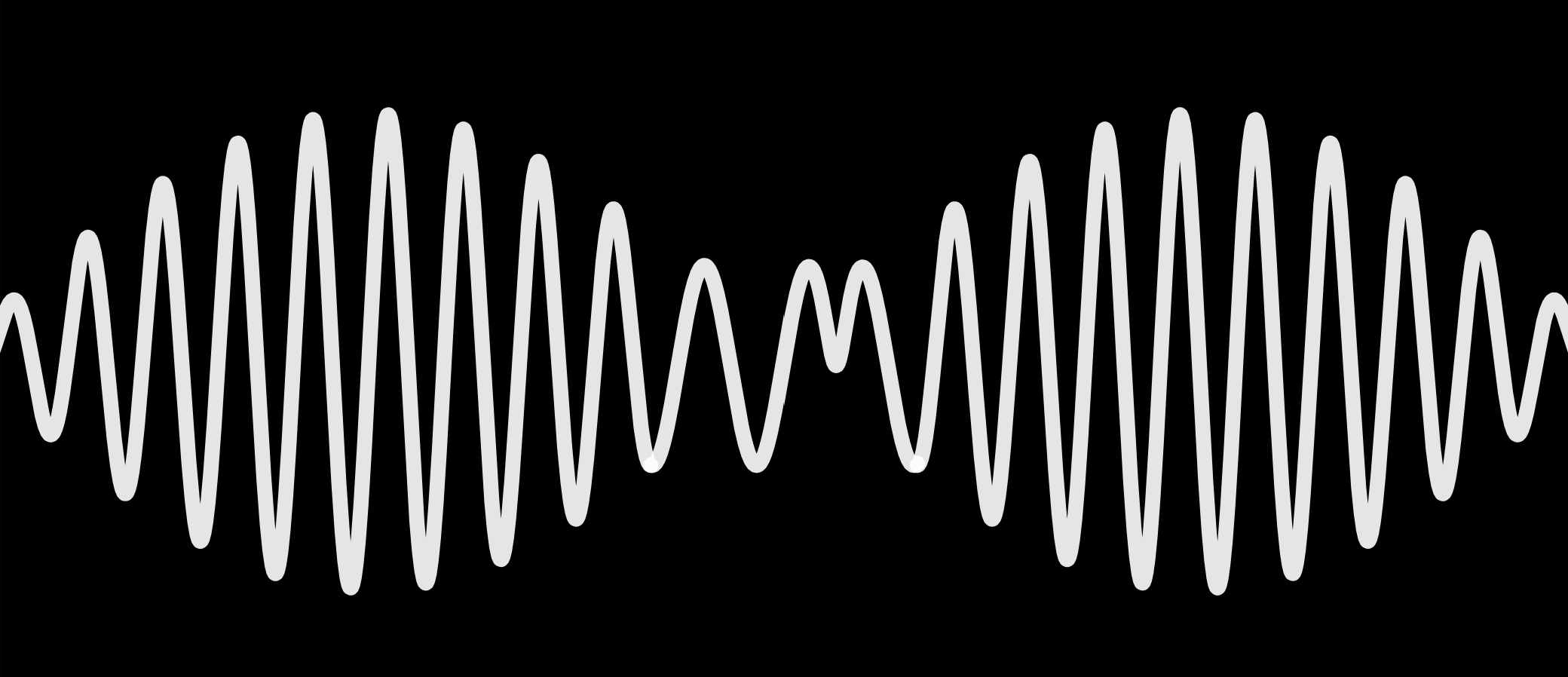
A few minutes ago, I was perfectly happy with this result, but that is no longer the case. Yes, I completed what I set out to do, but the closer I get, the farther I feel. The M needs to be more rectangular. My approximation isn’t actually a continuous function, much less a differentiable one. Looking at the two side-by-side, I can no longer see their similarities, only their differences. Recreating this cover art was supposed to be about a quick recreational math project, but now I feel obliged to honor this album. If imitation is the sincerest form of flattery, are better imitations more flattering?
After this project, I suppose not. By acknowledging the distance between my imitation and the original, I can do justice to the beauty it holds. I may have not recreated the cover perfectly, but I can certainly appreciate it much more now than I could when I first saw it. This is no Absent Minded Advanced Math. This is AM.
