People are often quick to dismiss infinity. For most, infinity represents some nebulous concept about going on forever or a number bigger than all the other numbers. Infinity is silly, hard to conceptualize, and just doesn’t matter for people living finite lives.
I tend to disagree. I think people underestimate just how useful infinity really can be. It has served me well for many years in countless situations. Then again, I did spend 4 years studying infinity, so I might be a tad biased.
One particular application of infinity comes up infrequently in origami. Every origami design starts with a finite sheet of paper. But why let that limit you? What if you could design a tree with infinite branches? A dinousaur with infinite ridges? A flower with infinite petals? No one really asked, but origamists answered anyway.
For every origami design, you can draw out on a flat sheet which part of the paper is used for each feature of the finished model. To fit an infinite number of features onto a single square, origamists needed a way to add an infinite number of things and end with a finite sum. Luckily, mathematicians have been doing this for centuries. One of the most common ways to add an infinite amount of stuff and end up with a finite amount is a geometric series.
Start by placing your finger on the left side of your screen. Next, move it halfway to the right side. Now, move it halfway between where it is now and the right side. Move it halfway again. And again. And again. If you continue this forever, your finger will take an infinite number of steps, but the lengths of those steps only add up to the width of your screen. This is a geometric series. Every subsequent step is some fixed fraction of the previous step.
Since origamists work in two dimensions, not just one, their steps get to look a little different. Take, for example, Shuzo Fujimoto’s hydrangea. At every step, the folder can add four more petals to the center of the flower. This sounds impossible, but I’ve drawn out how the paper is distributed for each petal. The red squares are the petals.
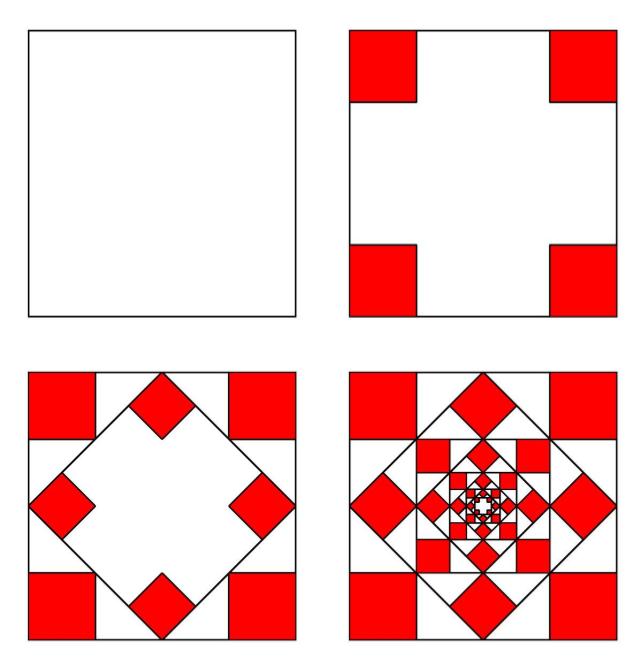
The progressive distribution of paper for the petals of Fujimoto’s Hydrangea. Note how each layer repeats the previous but in half the area.
Theoretically, this would result in an infinite number of petals, but that would require perfect paper, immortality, and a few other impossibilities. In practice, it means origamists can add as many petals as they like to their hydrangea. Each subsequent layer is a recursive iteration of the previous. It is, as Ushio Ikegami describes it, “an infinite set of origami works.” The artist defines a recursive sequence that allows folders to continue from one work to the next. That way, it goes on forever.
Infinite origami is technically impossible. The heat death of the universe will consume all attempts at folding forever. But that doesn’t stop origamists from trying. Using their incredible skills—and a bit of math—they have created endless art. They found infinity in a square. Where will you find it?
